Neste artigo, mostro o quanto os juros compostos são benéficos e muito importantes para a nossa vida financeira.
Os juros compostos são mais que nossos aliados, como afirmou Albert Einstein, um dos maiores gênios da humanidade:
“O juro composto é a oitava maravilha do mundo”.
Se Albert Einstein afirmou isso, com certeza eles devem ter algo de muito especial, não é verdade?
Os juros compostos já estão presentes em sua vida, más você nem se dá conta disso, eles estão embutidos tanto na rentabilidade de seus investimentos, quanto nas dívidas que você contrai.
Tudo isso deixa claro como é extremamente importante entender como funciona essa importante ferramenta, e procurar tirar o máximo de benefícios dela, não é mesmo?
Então fique comigo até o final desse post, e vamos desvendar juntos os segredos dos juros compostos, ok?
Vamos lá?
Índice Automático.
Juros Compostos - O que são?
Vou procurar explicar da forma mais simples, eficiente, e fácil de entender, ok?
A melhor definição de juros compostos é: “Juros sobre juros”.
Com essa definição fica bem fácil entender como eles funcionam.
A diferença entre juro simples, e juro composto.
A maior diferença entre o juro simples e o juro composto é que o juro simples é sempre calculado com base no valor do aporte inicial, e o juro composto é calculado com base no resultado imediatamente anterior, em que já foi incidido o juro.
Ou seja, o cálculo é sobre o resultado em que já foram adicionados juros.
Com isso, também existem diferenças nas fórmulas, onde no juro simples, o período é linear, já no juro composto o período é exponencial.
Fórmula do juro simples: M = C x i x t
Fórmula dos juros compostos: M = C (1 + i) t
Onde:
M = Montante final;
C = Capital inicial;
i = Taxa de juros fixa;
t = Tempo.
Veja nesse exemplo como é simples entender a diferença entre juros simples e juros compostos:
Imagine que você quer fazer um investimento de R$ 20.000 por 5 anos, a juros de 10% ao ano.
# Os $ 10.000 reais são o seu aporte inicial;
# Os 10 anos são o período que você quer deixar investido;
# E os 10% ao ano são os juros (seu prêmio) por investir seu dinheiro, certo?
Se os juros forem calculados somente sobre o aporte inicial de $ 10 mil, e isso todos os anos, esse cálculo se classifica como juros simples.
Veja como ficaria o cálculo e o rendimento no final do período:
Ano | Capital principal investido | Juros ao final do ano | Total do capital após 1 ano | Total dos juros acumulados |
1 | R$ 10.000 | R$ 1.000 | R$ 11.000 | R$ 1.000 |
2 | R$ 11.000 | R$ 1.000 | R$ 12.000 | R$ 2.000 |
3 | R$ 12.000 | R$ 1.000 | R$ 13.000 | R$ 3.000 |
4 | R$ 13.000 | R$ 1.000 | R$ 14.000 | R$ 4.000 |
5 | R$ 14.000 | R$ 1.000 | R$ 15.000 | R$ 5.000 |
6 | R$ 15.000 | R$ 1.000 | R$ 16.000 | R$ 6.000 |
7 | R$ 16.000 | R$ 1.000 | R$ 17.000 | R$ 7.000 |
8 | R$ 17.000 | R$ 1.000 | R$ 18.000 | R$ 8.000 |
9 | R$ 18.000 | R$ 1.000 | R$ 19.000 | R$ 9.000 |
10 | R$ 19.000 | R$ 1.000 | R$ 20.000 | R$ 10.000 |
Note que pelos juros simples, sempre serão adicionados $ 1.000 reais após todo final de ano.
Estes R$ 1.000 foram gerados a partir do capital inicial de R$ 10.000 x 10% (taxa de juros).
No final do primeiro ano, já somado o primeiro rendimento, o seu dinheiro aplicado será de R$ 11.000.
No segundo ano, os 10% continuarão incidindo somente sobre o aporte inicial de R$ 10.000, e assim por diante, ano após ano.
Esse é o juro simples.
Perceba que ao final do investimento você receberá R$ 10.000 de retorno total.
Ou seja, em 10 anos você dobrará o seu capital.
Fácil de entender, não é?
Agora perceba a diferença do cálculo sobre o mesmos valores e período, más, agora aplicando os juros compostos:
Ano | Capital principal investido | Juros ao final do ano | Total do capital após 1 ano | Total dos juros acumulados |
1 | R$ 10.000 | R$ 1.000 | R$ 11.000 | R$ 1.000 |
2 | R$ 11.000 | R$ 1.100 | R$ 12.100 | R$ 2.100 |
3 | R$ 12.100 | R$ 1.210 | R$ 13.310 | R$ 3.310 |
4 | R$ 13.310 | R$ 1.331 | R$ 14.641 | R$ 4.641 |
5 | R$ 14.641 | R$ 1.464 | R$ 16.105 | R$ 6.105 |
6 | R$ 16.105 | R$ 1.611 | R$ 17.716 | R$ 7.716 |
7 | R$ 17.716 | R$ 1.772 | R$ 19.487 | R$ 9.488 |
8 | R$ 19.487 | R$ 1.949 | R$ 21.436 | R$ 11.437 |
9 | R$ 21.436 | R$ 2.144 | R$ 23.579 | R$ 13.581 |
10 | R$ 23.579 | R$ 2.358 | R$ 25.937 | R$ 15.939 |
Perceba que com a aplicação dos juros compostos, o cálculo e os resultados são bem diferentes.
No Ano 1 os juros são de R$ 1.000, que é o resultado de (10.000 x 10%).
Más, no Ano 2 os juros incidem sobre o montante em que já foram somados os juros do mês anterior.
Portanto, os juros de R$ 1.100 é o resultado de (11.000 x 10%).
Já no ano 3 os juros de R$ 1.210, são o resultado de (12.100 x 10%).
E assim sucessivamente.
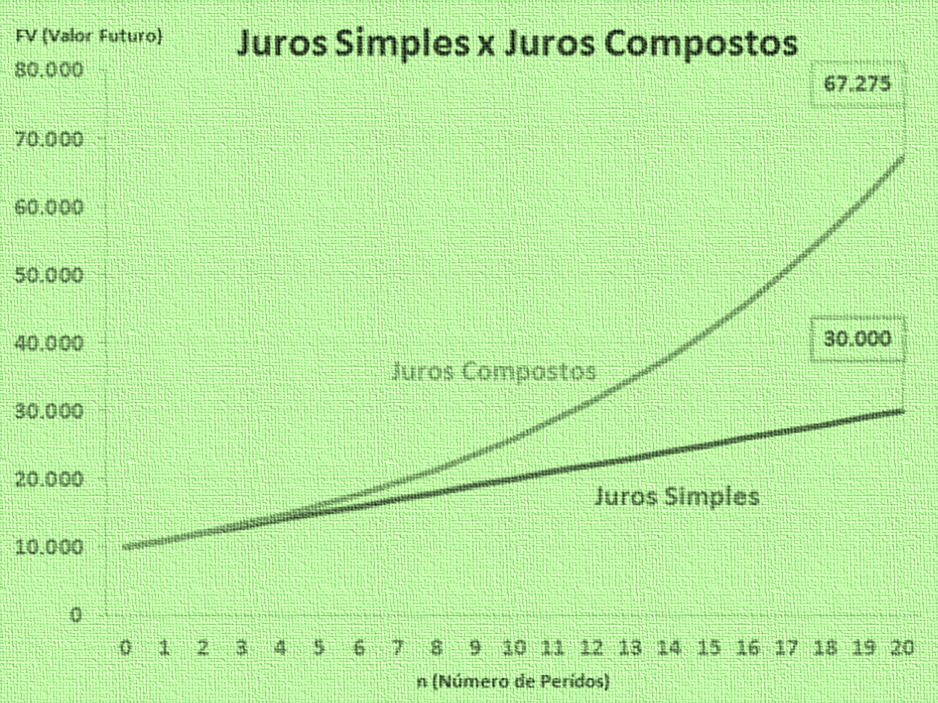
Perceba que a diferença mais importante entre os dois tipos de juros está na diferença da velocidade de crescimento entre eles.
Enquanto o crescimento dos Juros Simples é linear, ou seja, em linha reta, o crescimento dos Juros Compostos é exponencial, ou seja, o crescimento é baseado em percentual conforme o tempo passa.
Com isso, percebemos que, quanto maior o tempo em que deixarmos os juros compostos agirem, maior será a sua força e sua velocidade de geração de capital.
Esse fenômeno fica bem claro quando comparamos as velocidades de aumento entre as curvas através de um gráfico:
Juros Compostos - Para que servem?

Como dito no início do post, os juros compostos já estão presente em nossas vidas, más muitas vezes nem sabemos.
Ou seja, desde juros que conseguimos através de nossos investimentos, até os juros que pagamos quando contraímos empréstimos são influenciados pelos juros compostos.
Portanto, se você entendeu bem o que expliquei anteriormente, já deve ter percebi quais são os lados, positivo e negativo, dos juros compostos.
O lado positivo é que podemos utilizar todos os benefícios dos juros compostos a nosso favor através dos investimentos.
Pois devido à sua característica exponencial, nosso dinheiro irá se valorizar mais rápido se deixarmos os juros compostos agirem sobre ele.
Algumas modalidades de investimento em renda fixa, têm seus juros (prêmio) calculados com base em juros sobre juros.
Más, investimentos em renda variável, como no caso das ações, também podem ser beneficiados com a ajuda dos juros compostos.
Podemos fazer isso reinvestindo os ganhos obtidos com as ações, sejam eles através dos proventos, ou através das bonificações, ou até mesmo pelos ganhos de capital obtidos com a valorização das ações.
Nesse último caso, após a ação se valorizar bem, podemos vende-las, em seguida aguardar por uma queda mais forte, e então recomprar ainda mais ações, da mesma empresa, más por um valor bem mais baixo.
Isso permitirá que compremos uma quantidade maior de ações, o que por sua vez, nos dará direito a receber ainda mais proventos e bonificações.
Se fizermos isso por um longo período, também, deixaremos os juros compostos agirem, entendeu?
Em contra partida, como você já pode imaginar, da mesma forma que os juros compostos são benéficos quando os utilizamos para ganhar juros com os investimentos, eles são muito prejudiciais se fizermos dívidas cujos juros forem baseados em juros compostos.
Ou seja, a dívida baseada em juros compostos também tenderá a aumentar exponencialmente caso não paguemos as prestações em dia.
Diante desses fatos, raciocine comigo.
Em qual dos dois lados é melhor focar e agir? Do lado de ganhar os juros compostos? Ou, pagar juros compostos?
Fácil de deduzir, não é?
Acredito que esses argumentos já sejam suficientes para convencer você sobre o poder de geração de capital dos juros compostos.
Principalmente sobre o seu poder em nos ajudar a tingir a independência financeira mais rápido.
Entendido esses pontos, vamos em frente.
Juros Compostos - Como Calcular?
De modo geral, o conhecimento sobre as fórmulas tem um cunho mais didático.
Serve para compreendermos melhor a dinâmica dos cálculos, pois no dia a dia dificilmente você calculará manualmente.
Porque nos dias de hoje, existem várias ferramentas disponíveis para calcularmos os juros compostos, nas próprias instituições financeiras, como o próprio tesouro direto, ferramentas em sites, planilhas e a própria calculadora financeira.
Para o cálculo dos juros compostos podemos utilizar várias fórmulas, ou nomear as variantes das fórmulas de várias formas diferentes.
Más, nesse exemplo, vou utilizar a fórmula mais simples e mais utilizada no Brasil que é:
M = C (1 + i) t
Portanto, nessa fórmula existem quatro variáveis:
M = Montante final;
C = Capital inicial;
i = Taxa de juros fixa;
t = Tempo.
Temos que nos atentar para alguns detalhes muito importantes para que o cálculo seja feito corretamente.
Um desses detalhes é inserir a taxa de juros em valor decimal.
Ou seja, se o juro é de 10%, em (i), escreva 0,1.
Chegamos ao valor decimal dividindo o valor da taxa de juros por 100.
Ou seja, 10 ÷ 100 = 0,1.
Outro detalhe muito importante é, utilizar a taxa de juro correta, que é referente ao tempo utilizado.
Ou seja, se o período a ser aplicado será de, por exemplo 18 meses, utilize a taxa de juro mensal.
Se a taxa de juros for anual, transforme a quantidade de meses em anos, por exemplo 24 meses = 2 anos.
Voltando às fórmulas, através de sua alteração é possível obter a resposta para qualquer uma das variáveis.
Más, para calcular os juros compostos é necessário conhecer o capital inicial e o montante final, pois o resultado do investimento é gerado pela diferença entre os dois.
Exemplo de cálculo:
Um capital de R$ 15.000 foi aplicado a juros compostos em um fundo de investimento que rende 7% a.a.
Qual será os juros acumulados em 36 meses?
Resolução:
Dados:
C = 15.000;
i = 7% a.a.;
t = 36 meses.
Lembrando dos detalhes, temos que colocar o “tempo” na mesma taxa utilizada, que é anual.
Ou seja, t= 3 anos.
Temos que converter também a taxa para decimal.
Portanto i= 0,07.
Calculando:
M = C (1 + i) t
M = 15.000 (1 + 0,07) 3
M = 15.000 (1,07) 3
M = 15.000 x 1,2250
M = 18.375
Para encontrarmos o juro total ficam:
J = M – C
18.375 – 15.000 = 3.375
Exemplos de ferramentas digitais:
Como calcular no Excel?
As variáveis para calcular os juros compostos pelo Excel são as mesmas, o que muda são as formas de se calcular, porque o Excel tem várias fórmulas diferentes para os juros compostos.
De modo geral faça como o exemplo abaixo:
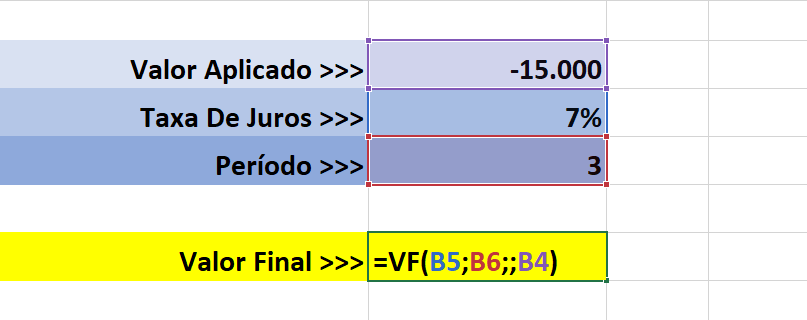
Escreva cada um dos dados separadamente em cada linha.
Obs.: Na célula referente ao aplicado (Valor Presente), insira o número com sinal de (-).
Na última célula, insira a fórmula do valor final, iniciando sempre pelo sinal de (=), as letras da fórmula (VF), e selecione as células com os dados separados por (;) como na imagem abaixo:
Obs.: Se não tiver todos dados solicitados da fórmula, coloque (;) para completar.
Em seguida, após selecionar as células clique em “enter”, a fórmula será finalizada e apresentará o resultado do cálculo, como apresentado abaixo:

Como calcular na calculadora HP12c?
Podemos também utilizar uma calculadora financeira para fazer o cálculo dos juros compostos.
Uma das calculadoras mais conhecidas é a HP 12c.
Inclusive podemos fazer os cálculos através de sua versão online, que é um emulador da HP 12c.
Vamos ver agora o passo a passo para o calcular através da HP 12c.
1- Primeiramente clique em f + FIN para limpar o histórico de registros.

2- Em seguida, insira o valor inicial, depois clique em + CHS + PV. O botão (CHS) serve para inserir o valor em negativo, e o (PV) informa que esse é o valor inicial.

3- A seguir, informe o período da aplicação. Digite o número de períodos, em seguida clique no botão (n).

4- O próximo passo é inserir o valor da taxa de juros. Insira o valor e pressione a tecla (i).

Por fim, se tudo estiver certo, após clicar na tecla (FV), o valor dos juros compostos já aparecerá corretamente.

Conclusão.

Bem amigo (a), a mensagem mais forte que posso deixar para você hoje é, comece o mais rápido possível a usar os juros compostos a seu favor.
Como vimos, para retirar o máximo de proveito dos juros compostos, temos que ter conhecimento, paciência e disciplina.
Com isso, convido você a ampliar seus conhecimentos explorando os artigos do site.
Veja o exemplo de alguns artigos com temas muito importantes:
Você também pode aprender mais sobre tipos de investimentos de menor risco, em que os juros compostos podem ser utilizados com eficiência, como é o caso do tesouro direto.
Más, sendo muito sincero, você só verá seu patrimônio crescer significativamente, após você aprender a utilizar o poder dos juros compostos através do mercado de ações.
Se você estiver interessado em começar a investir nessa modalidade, recomendo que conheça a forma como opero no mercado de ações através de um método seguro, tranquilo e muito eficiente.
Saiba mais a respeito desse método através do post Aprenda Como Investir Em Ações.
E se você tiver mais alguma dúvida sobre juros compostos, deixe o seu comentário logo abaixo, ou, entre em contato pelo formulário, responderemos o mais breve possível, ok?
Muito obrigado pelo seu tempo!
Forte Abraço.